Hexo
0%

博弈论

Posted on In ,
Symbols count in article: 8.6k Reading time ≈ 8 mins.

博弈论

公平组合游戏

  • 由两名玩家交替行动
  • 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关
  • 游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束

尼姆游戏

给定 N堆物品，第 i 堆物品有 $a_i$个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜

结论：定义 Nim 和为$a_1\oplus a_2\oplus a_3…\oplus a_n$,当且仅当 Nim和为 0 时，该状态为先手必败状态 否则该状态为先手必胜状态

巴什博弈

有 1 堆石子，总个数是 n ，两名玩家轮流在石子堆中拿石子，每次至少取 1 个，至多取 m 个。取走最后一个石子的玩家为胜者。判定先手和后手谁胜。

结论： 若 n%(m+1)==0 ，则先手获胜，否则后手获胜

威佐夫博弈

有两堆石子，石子数可以不同。两人轮流取石子，每次可以在一堆中取，或者从两堆中取走相同个数的石子，数量不限，取走最后一个石头的人获胜。判定先手是否必胜。

1
2
3
4
5
6
7
8
9
10
11
12
int main() {
	scanf("%d%d", &n, &m);
    if (a > b)
        swap(a, b);
    int ans = (b - a) * ((1.0 + sqrt(5.0)) / 2.0);
    if (ans == a)
        puts("0");
    else
        puts("1");
    return 0;
}

斐波那契博弈

有一堆个数为 n ( n ≥ 2 ) n(n\ge 2)n(n≥2)的石子，游戏双方轮流取石子，规则如下：

先手不能在第一次把所有的石子取完，至少取 1 11 颗；

之后每次可以取的石子数至少为 1 11，至多为对手刚取的石子数的 2 22 倍。

约定取走最后一个石子的人为赢家，求必败态

结论：先手必败，当且仅当石子数为斐波那契数

SG函数

Mex运算

设 S 表示一个非负整数集合。定义 mex(S) 为求出不属于集合 S 的最小非负整数的运算。

SG函数

SG(终点) = 0

img

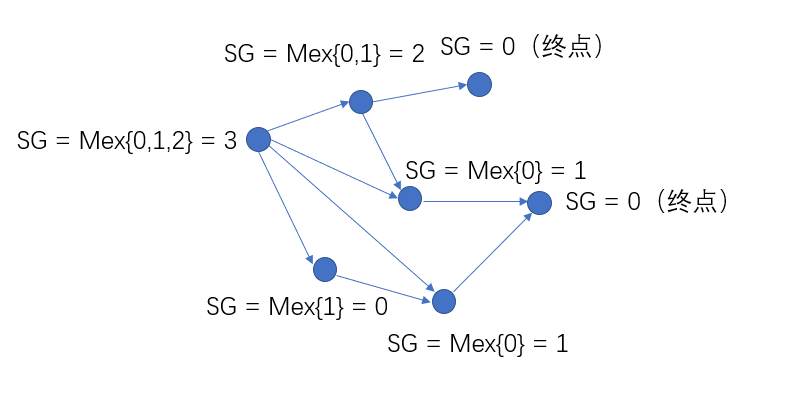
若SG(x) = 0则为必败状态，若SG(x) != 0,则为必胜状态

  • 对于任意的局面，如果它的SG值为0，那么他的任何一个后继局面的SG值不为0
  • 对于任意的局面，如果它的SG值不为0，那么她一定有一个后继局面的SG值为0

SG定理

有一般胜利下的公平组合游戏都能转化成尼姆数表达的尼姆堆博弈，一个博弈的 尼姆值 定义为这个博弈的等价尼姆数，即：对于当前游戏 X ，它可以拆分成若干个子游戏 $x_1,x_2,x_3…x_n$，那么$SG(X) = SG(X_1)\oplus SG(X_2)\oplus SG(X_3)\oplus …\oplus SG(X_N)$

对于由 n nn 个有向图游戏组成的组合游戏 设它们的起点分别为$x_1,x_2,x_3…x_n$，那么仅当$SG(X_1)\oplus SG(X_2)\oplus SG(X_3)\oplus …\oplus SG(N) ！= 0$时，这个游戏为先手必胜

有向图游戏的和

设$G_1,G_2,…G_n$是 n 个有向图游戏。定义有向图游戏 G， 他的行动规则是任选某个有向图$G_i$，并在$G_i$上行动一步。G被称为有向图游戏

有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和

$SG(G) = SG(G_1)\oplus SG(G_2)\oplus SG(G_3)\oplus …\oplus SG(G_N)$

  • 有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0
  • 有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0

sample

给定n堆石子以及一个由k个不同正整数构成的数字集合S。现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合S，最后无法进行操作的人视为失败。问如果两人都采用最优策略，先手是否必胜。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;
int n,m;
int s[105],f[10005];
int sg(int x){
    if(f[x] != -1)  return f[x];
    unordered_set<int> S;
    for(int i = 0;i < m;i++){
        int sum = s[i];
        if(x >= sum)    S.insert(sg(x - sum));
    }
    for(int i = 0;;i++){
        if(!S.count(i)) return f[x] = i;
    }
}
int main(){
    cin>>m;//m个数量选择
    for(int i = 0;i < m;i++)    cin>>s[i];
    cin>>n;//n堆石子
    memset(f,-1,sizeof f);
    int x,res = 0;
    for(int i = 0;i < n;i++){
        cin>>x;
        res ^= sg(x);
    }
   if(res) puts("Yes");
    else    puts("No");
    return 0;
}

SG游戏及其变形

Anti-SG 游戏（走完最后一步者输）

Anti-Nim

有 n 堆石子，两个人可以从任意一堆石子中拿任意多个石子(不能不拿)，拿走最后一个石子的人失败。问谁会胜利

结论：先手必胜当且仅当

  • 所有堆的石子数都为 1且游戏的SG值为 0
  • 有些堆的石子数大于 1且游戏的SG值不为 0

Anti-SG

决策集合为空的游戏者获胜，也可以理解将所有集合变为空的游戏者即为失败。

其余规则与普通的 SG 游戏相同。

SJ定理：先手必胜当且仅当

  • 游戏的 SG 函数值不为 0 且游戏中某个单一游戏的 SG 函数值大于 1
  • **游戏的SG函数值为 0 且游戏中没有任意一个单一游戏的SG函数值大于 1 **

Multi-SG

可以将一堆石子分成多堆

Multi-Nim

有 n 堆石子，两个人可以从任意一堆石子中拿任意多个石子（不能不拿）或者可以把一堆数量不少于 2石子堆分为两堆不为空的石子堆，没法拿的人失败。问谁会胜利。

性质：

1
2
3
4
5
6
if(x%4==0)
SG(x) = x-1;
else if(x%4==1||x%2==2)
SG(x)=x;
else if(x%4==3)
SG(x)=x+1;

Multi-SG

每次操作能将一个当前的单一游戏分为多个单一游戏，也就是将当前这个堆石子分为多堆石子的特殊游戏。

翻硬币游戏

N 枚硬币排成一排，有的正面朝上，有的反面朝上。我们从左开始对硬币按1 到N 编号。

第一，游戏者根据某些约束翻硬币，但他所翻动的硬币中，最右边那个硬币的必须是从正面翻到反面。例如，只能翻3个硬币的情况，那么第三个硬币必须是从正面翻到反面。如果局面是正正反，那就不能翻硬币了，因为第三个是反的。

第二，谁不能翻谁输。

有这样的结论：局面的SG 值为局面中每个正面朝上的棋子单一存在时的SG 值的异或和。即一个有k个硬币朝上，朝上硬币位置分布在的翻硬币游戏中，SG值是等于k个独立的开始时只有一个硬币朝上的翻硬币游戏的SG值异或和。比如THHTTH这个游戏中，2号、3号、6号位是朝上的，它等价于TH、TTH、TTTTTH三个游戏和，即sg[THHTTH]=sg[TH]⨁sg[TTH]⨁sg[TTTTTH]��[������]=��[��]⨁��[���]⨁��[������].我们的重点就可以放在单个硬币朝上时的SG值的求法。

约束条件一：每次只能翻一个硬币。

一般规则中，所翻硬币的最右边必须是从正面翻到反面，因为这题是只能翻一个硬币，那么这个硬币就是最右边的硬币，所以，每次操作是挑选一个正面的硬币翻成背面。

对于任意一个正面的硬币，SG值为1。

有奇数个正面硬币，局面的SG值 == 1，先手必胜，有偶数个正面硬币，局面的SG值 == 0，先手必败

约束条件二：每次能翻转一个或两个硬币。(不用连续)

每个硬币的SG值为它的编号，初始编号为1，可以转化为NIM游戏

如果对于一个局面，把正面硬币的SG值异或起来不等于0，既a1 ^ a2 ^ a3 ^ … ^ an == x,

那么玩家必然可以通过翻转一个或两个硬币使得异或和为0
证明：不妨设x的二进制表示中最高一位1在第k位，那么在a1,a2,…,an中，必然有一个数ai，它的第k位是1，且ai’ = ai ^ x<ai，

如果 ai’ == 0，意思就是说，把 ai 这个值从式子中去掉就可以了。对应游戏，就是把编号为ai’的正面硬币翻成背面就可以了。

如果ai’ !=0，意思就是说，把 ai 这个值从式子中去掉后再在式子中加上ai’。对应游戏，去掉ai’就是把编号为ai的正面硬币翻成背面，加上ai’ ，如果编号为ai’ 的硬币是正面，我们就把它翻成背面，是背面就翻成正面，总之，就是翻转编号为ai’ 的硬币。

约束条件三：每次必须连续翻转k个硬币。

可以转化为巴什博弈

我们计算的是个数为N的硬币中，当中最后一个硬币为正面朝上,的sg值。

当N==1时。硬币为：正，先手必输，所以sg[1]=0。

当N==2时，硬币为：反正。先手必输，所以sg[2]=0。

当N==3时，硬币为：反反正，先手必胜。所以sg[3]=1。

当N==4时，硬币为：反反反正。先手操作后为：反正正反，子状态局面的SG=0^1=1，那么sg[4]=0。

当N==5时，硬币为：反反反反正。先手操作后为：反反正正反。子状态局面的SG=1^0=1。那么sg[5]=0。

当N==6时，硬币为：反反反反反正。先手操作后为：反反反正正反。子状态局面的SG=0^0=0。那么sg[6]=1。

依据观察，能够知道:从编号为1开始，sg值为：001 001 001 001……

依据观察，能够知道，sg的形式为000…01 000…01，当中一小段0的个数为k-1。

约束条件4：每次翻动一个硬币后。必须翻动其左侧三个硬币中的一个，即翻动第x个硬币后。必须选择x-1。x-2，x-3中的当中一个硬币进行翻动，除非x是小于等于3的。（Subtraction Games）

还是可以转化为类似巴什博弈的模型

当N == 1时，硬币为：正，先手必赢，所以sg[1]=1。

当N == 2时。硬币为：反正，先手必赢，由于先手能够翻成反反或正反。可能性为2。所以sg[2] == 2。

当N == 3时，硬币为：反反正，先手操作后能够为：反正

位置x：1 2 3 4 5 6 7 8 9 10 11 12 13 14…

sg[x]： 1 2 3 0 1 2 3 0 1 2 3 0 1 2…

这个与每次最多仅仅能取3个石子的取石子游戏的SG分布一样，相同还有相似的这类游戏，约束条件5也是一样。

约束条件5：每次必须翻动两个硬币，并且这两个硬币的距离要在可行集S={1,2,3}中。硬币序号从0开始。(Twins游戏)

当N == 1时，硬币为：正，先手必输，所以sg[0]=0。

当N == 2时，硬币为：反正，先手必赢。所以sg[1]=1。

当N == 3时。硬币为：反反正。先手必赢，所以sg[2]=2。

当N == 4时，硬币为：反反反正，先手必赢，所以sg[3]=3。

当N == 5时。硬币为：反反反反正，先手必输，所以sg[4]=0。

位置x：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14…

sg[x]： 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2…

约束条件6：每次能够翻动一个、二个或三个硬币（Mock Turtles游戏）

初始编号从0开始。

当N==1时。硬币为：正，先手必胜，所以sg[0]=1.

当N==2时，硬币为：反正，先手必赢，先手操作后可能为：反反或正反，方案数为2，所以sg[1]=2。

当N==3时，硬币为：反反正。先手必赢，先手操作后可能为：反反反、反正反、正反正、正正反。方案数为4。所以sg[2]=4。

位置x：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14…

sg[x]： 1 2 4 7 8 11 13 14 16 19 21 22 25 26 28…

看上去sg值为2x或者2x+1。

下面引入一个概念：我们称一个非负整数为odious，当且仅当该数的二进制形式的1出现的次数是奇数，否则称作evil。

所以1，2，4，7是odious，因为它们的二进制形式是1,10,100,111。而0,3,5,6是evil，由于它们的二进制形式是0,11,101,110。

而上面那个表中。貌似sg值都是odious数。所以当2x为odious时，sg值是2x，当2x是evil时。sg值是2x+1.

这样怎么证明呢？我们会发现发现：

evil ^ evil = odious ^ odious = evil

evil ^ odious = odious ^ evil = odious

如果刚才的假说是成立的，我们想证明下一个sg值为下一个odious数。注意到我们总能够在第x位置翻转硬币到达sg为0的情况；通过翻转第x位置的硬币和两个其他硬币。我们能够移动到全部较小的evil数，由于每一个非零的evil数都能够由两个odious数异或得到。可是我们不能移动到下一个odious数，由于不论什么两个odious数的异或都是evil数。

假设在一个Mock Turtles游戏中的首正硬币位置x1,x2,…,xn是个P局面。即sg[x1]…sg[xn]=0.那么无可置疑的是n必然是偶数，由于奇数个odious数的异或是odious数，不可能等于0。而由上面可知sg[x]是2x或者2x+1，sg[x]又是偶数个，那么x1 ^ x 2 ^ …^ xn = 0。相反，假设x1 ^ x 2 ^ … ^ xn = 0且n是偶数，那么sg[x1] ^ … ^ sg[xn]=0。这个假设不太理解的话，我们能够先这么看下：2x在二进制其中相当于把x所有左移一位，然后补零，比方说2的二进制是10。那么4的二进制就是100。而2x+1在二进制其中相当于把x所有左移一位，然后补1，比方说2的二进制是10，5的二进制是101。如今看下sg[x1] ^ … ^ sg[xn]=0，由于sg[x]是2x或者2x+1。所以式子中的2x+1必须是偶数个（由于2x的最后一位都是0,2x+1的最后一位都是1，要最后异或为0,2x+1必须出现偶数次），所以:MT游戏其中的P局面是拥有偶数堆石子的Nim游戏的P局面。

其实只需要记住MT游戏中每个位置的sg为对应的odious数（2x或2x+1）即可

约束条件7：每次能够连续翻动随意个硬币，至少翻一个。（Ruler游戏）

初始编号从1开始。

那么这个游戏的SG函数是g(n)=mex{0,g(n-1),g(n-1) ^ g(n-2),…,g(n-1) ^ … ^ g(1)}

依据SG函数能够得到SG值表例如下：

位置x：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16…

g(x): 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16…

所以sg值为x的因数其中2的能达到的最大次幂。比方14=2 * 7，最大1次幂。即2；16=2 * 2 * 2 * 2。最大4次幂，即16。

这个游戏成为尺子游戏是由于SG函数非常像尺子上的刻度。

约束条件8：每次必须翻转4个对称的硬币，最左与最右的硬币都必须是从正翻到反。（开始的时候两端都是正面）（Grunt游戏）

这是Grundy游戏的变种，初始编号从0开始。

当正硬币位置为0,1,2时是terminal局面，即 终结局面，sg值都是0。当正硬币位置n大于等于3的时候的局面能够通过翻0,x,n-x,n四个位置得到(当中x<n/2可保证胜利)。

这就像是把一堆石子分成两堆不同大小石子的游戏，也就是Grundy游戏。
小结：
遇到翻硬币问题，如果找不到现成的模型，可以尝试往现有的模型（如nim游戏、巴什博弈等转化），不行就暴力打表sg函数找规律即可

无向图删边

一、树的删边游戏

给出一棵有根树，两人轮流操作，每人每次可以选择一条边删去，不与根节点相连的部分将被移走。无法操作者输。

结论：叶子节点的 SGSG 值为 00；中间节点的 SGSG 值为它的所有子节点的「SGSG 值加 11」的异或和。这样就可以推出根节点的 SGSG 值。证明。

二、POJ 3710 Christmas Game

Description

有 n 个局部连通的图，两人轮流操作，每人每次可以选择一条边删去，不与根节点相连的部分将被移走。无法操作者输。（图是通过从基础树上加一些边得到的，环与环之间无公共边，且只与基础树有一个公共点。）

Solution

与「树的删边游戏」不同的在于图中 出现了环。所以环可以单独考虑。

分析环的性质：环保证不共用边，且只与基础树有一个公共点。因此所有的环都是从树中某一个点连出又连回同一个点的简单环。

  • 对于长度为奇数的环，去掉其中任意一条边后，剩下的两个链长度 同奇偶，异或之后的 SG 值不可能为奇数，并且可能为 00。所以进行 mex 运算后它的 SG 值为 11。

  • 对于长度为奇数的环，去掉其中任意一条边后，剩下的两个链长度 不同奇偶，异或之后的 SG 值不可能为 0。所以进行 mex 运算后它的 SG 值为 0。实际上它并没有贡献。

所以可以去掉所有的偶环，将所有的奇环变为长度为 1 的链，转化为「树的删边游戏」的模型。

算出每一棵树的 SG 值，再把所有根节点的 SG 值异或起来即可。

具体实现时，不需要做「将所有的奇环变为长度为 1 的链」的操作，只需考虑奇环的贡献。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<cstdio>
#define int long long
using namespace std;
const int N=1e5+5;
int t,n,m,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],top,s[N],sg[N],vis[N],ans;    //vis=0: 未访问过  vis=1: 访问过且不是某个环上的点（不考虑树上的点）  vis=-1: 访问过且是某个环上的点 
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void dfs(int x,int fa){
    s[++top]=x,vis[x]=1,sg[x]=0;
    bool flag=0;
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa&&!flag){flag=1;continue;}     //第一次连向父节点 
        if(vis[y]==1){
            int cnt=1,now=x;
            while(now!=y) cnt++,vis[now]=-1,now=s[--top];
            if(cnt&1) sg[y]^=1;    //奇环 
        }
        else if(!vis[y]){
            dfs(y,x);
            if(~vis[y]) sg[x]^=(sg[y]+1);    //不在环上的才能更新 
        }
    }
    if(~vis[x]) --top;    //非环上的，及时出栈 
}
signed main(){
    while(~scanf("%lld",&t)){
        ans=0;
        while(t--){
            scanf("%lld%lld",&n,&m),cnt=top=0;
            for(int i=1;i<=n;i++) hd[i]=vis[i]=0;
            for(int i=1;i<=m;i++){
                scanf("%lld%lld",&x,&y);
                add(x,y),add(y,x);
            }
            dfs(1,0),ans^=sg[1];    //根节点的 SG 值异或起来 
        }
        puts(ans?"Sally":"Harry");
    }
    return 0;
}